|
Poslao: 12 Dec 2012 01:08
|
offline
- Pridružio: 08 Maj 2008
- Poruke: 66
|
Problem je sledeci:
Neka su a i b realni brojevi.
a+a+...+a (b puta) mozemo zapisati kao a*b.
a*a*...*a (b puta) mozemo napisati kao a^b.
Da li je moguce podici a na a, b puta? Kao sto mozemo podici a na a, x puta (x je ceo broj), da li to moze da se uradi ne-ceo broj puta, dakle a^a^a^...^a (b puta)?
|
|
|
|
|
Registruj se da bi učestvovao u diskusiji. Registrovanim korisnicima se NE prikazuju reklame unutar poruka.
|
|
|
Poslao: 12 Dec 2012 08:43
|
offline
- vasa.93

- Moderator foruma

- Pridružio: 17 Dec 2007
- Poruke: 14825
- Gde živiš: Niš
|
Ajde objasni šta bi ti da bude u eksponentu? Daj neki konkretan primer.
|
|
|
|
|
|
|
Poslao: 12 Dec 2012 12:35
|
offline
- Pridružio: 15 Feb 2011
- Poruke: 157
- Gde živiš: Kovin
|
moze da se izracuna a^x za svaki realan broj x, pod uslovom a > 0, ali to se ne radi na isti nacin kao stepenovanje sa celim brojem.
|
|
|
|
|
|
|
|
|
Poslao: 12 Dec 2012 14:21
|
offline
- azraelXYZ

- Zaslužni građanin

- Neću da ti kažem...
- ...gde preprodajem zjala.
- Pridružio: 05 Avg 2011
- Poruke: 663
- Gde živiš: Pored kontejnera. Čukni dva puta u poklopac, traži Raduleta.
|
može, ali se onda eksponent piše u obliku razlomka(ako sam dobro razumeo pitanje) 
|
|
|
|
|
|
|
Poslao: 12 Dec 2012 15:21
|
offline
- Pridružio: 15 Feb 2011
- Poruke: 157
- Gde živiš: Kovin
|
ne mora izlozilac da bude u obliku razlomka, moze recimo 2^(koren iz 2), ovde izlozilac nije razlomak jer je koren iz 2 iracionalan. inace, po definiciji, to se racuna kao limes od 2^x, kada x tezi u koren iz 2, s'time da x prolazi kroz skup racionalnih brojeva 
|
|
|
|
|
|
|
|
|
Poslao: 12 Dec 2012 16:09
|
offline
- imho

- Građanin
- Pridružio: 20 Nov 2012
- Poruke: 124
- Gde živiš: Belgrade, Serbia
|
Pitanje je, po meni, vrlo zanimljivo – da li je moguće stepenovati a samim sobom b puta, pri čemu b nije ceo broj.
Ako bismo postavili neku analogiju između ovog slučaja i množenja nekog broja samim sobom b puta, jeste moguće pomnožiti a samim sobom b puta, pri čemu b nije ceo broj, već je oblika m/n, gde su m i n celi brojevi. I to se obeležava kao a^(m/n), tj. n√(a^m) ili (n√a)^m (gde n√ označava n-ti koren).
Međutim, budući da kod množenja važi asocijativnost a kod stepenovanja ne važi, tj. (a^b)^c≠a^(b^c), nisam siguran da bi se slično razmišljanje moglo odnositi i na stepenovanje nekog broja samim sobom.
Zanimalo bi me da čujemo i druga mišljenja.
|
|
|
|
|
|
|
Poslao: 12 Dec 2012 16:38
|
offline
- vasa.93

- Moderator foruma

- Pridružio: 17 Dec 2007
- Poruke: 14825
- Gde živiš: Niš
|
vujic ::Da li je moguce podici a na a, b puta?Ovako nešto: 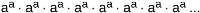 b puta?? b puta??
|
|
|
|
|
|
|
Poslao: 12 Dec 2012 16:48
|
offline
- imho

- Građanin
- Pridružio: 20 Nov 2012
- Poruke: 124
- Gde živiš: Belgrade, Serbia
|
Čovek je mislio na slučaj (...(((a^a)^a)^a)...)^a (pri čemu ima ukupno b stepenovanja).
|
|
|
|
|
|









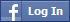




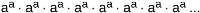 b puta??
b puta??

