Pomoć oko zadataka za prijemni.

• 0Niko još nije pohvalio poruku.
  Registruj se da bi pohvalio/la poruku!

Dobro jasno mi je.

• 0Niko još nije pohvalio poruku.
  Registruj se da bi pohvalio/la poruku!

Aleksandr1996 :: b) (5^2 - 3^3)^2 (kvadrat binoma) (5^2)^2 - 2*5^2*3^3 + (3^3)^2 = 625 - 1350 + 729 = 4


Izvini, potpuno je ispravno tvoje resenje, ali si ga zakomplikovao brate. Posto nisu nepoznate u pitanu, nego konkretni brojevi, nije potrebno koristiti obrazac za kvadrat binoma, nego samo izracunati. (25-27)^2=4

Poz.

• 0Niko još nije pohvalio poruku.
  Registruj se da bi pohvalio/la poruku!

Ti obrsci sluze za takvo racunaje da bi ga olaksali samo (A+B)^2 = A^2+2*A*B+B^2 kao takvo nista ne znaci ono opisuje kako se to (a+b )^2 rastavlja da bi se lakse doslo do rezultata. Samo sto se u osnovnoj skoli radi samo bez brojeva iz nekog razloga. Mada upravu si ovo je bilo bespotrebno komplikovanje nisam razmisljao cim vidim jedno resenje ne trazim drugo. Potrazi pascalov trougao, drugo ime za to je Njutnov binomni obrazac da bi shvatio (a+b)^2 pa onda na 3 itd Poz

• 0Niko još nije pohvalio poruku.
  Registruj se da bi pohvalio/la poruku!

Da je umesto kvadrata bilo ^9 bilo bi vrlo komplikovano da preko Binomnog obrasca da dobiješ da je rešenje (-2)^9 .

• 0Niko još nije pohvalio poruku.
  Registruj se da bi pohvalio/la poruku!

Budi siguran da znam to radio sam do (a+b)^20 ali ima i kraci nacin da se to uradi samo sto sam ga zaboravio pa ako neko zna nke mi javi .

• 1Ovo se svidja korisniku: Isidora01
  
  Registruj se da bi pohvalio/la poruku!

Aleksandr1996 ::Budi siguran da znam to radio sam do (a+b)^20 ali ima i kraci nacin da se to uradi samo sto sam ga zaboravio pa ako neko zna nke mi javi .
Postoji, zove se Paskalov trougao(piramida).

• 0Niko još nije pohvalio poruku.
  Registruj se da bi pohvalio/la poruku!

Lakše je preko Binomnog obrasca, jer kada radiš preko Paskalovog trougla moraš da znaš koje ćeš stepene da staviš, dok prilikom korišćenja Binomne formule to je šablosnki.

• 0Niko još nije pohvalio poruku.
  Registruj se da bi pohvalio/la poruku!

Napisano: 19 Feb 2012 17:33

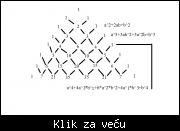
Sve je sablonski. mislim da ovako to izgleda nije bas najbolje jer je u paintu


Dopuna: 19 Feb 2012 17:39

kada imamo (a+b)^4=a^4+4a^3*b^1 to a^3 i b^1 vazno je da se stepeni kad se saberu iznose 4 posto je (a+b)^4 i imate ovde ono sto je saten napisala (a+b)^3 ovo se uci u 4 godini za gimnazije i nije za osnovnu skolu

• 0Niko još nije pohvalio poruku.
  Registruj se da bi pohvalio/la poruku!

Sherlock H. ::Lakše je preko Binomnog obrasca, jer kada radiš preko Paskalovog trougla moraš da znaš koje ćeš stepene da staviš, dok prilikom korišćenja Binomne formule to je šablosnki.
Zavisi od velicine eksponenta... Za vece je lakse nacrtati Paskalov trougao.

• 0Niko još nije pohvalio poruku.
  Registruj se da bi pohvalio/la poruku!

Aleksandr1996 ::Sta najvise volis od predmeta ako hoces informatiku zemunska je losa uprkos tome su profesori visoko obrazovani postdiplomske studije njih neinteresuje preterano neki dotatni rad sa prvacima. Ja sam pitao da ucimm programiranje ali ono ignorisali su me.

I u mojoj školi takođe nemam punu podršku od profesora što se tiče programiranja i takmičenja iz istog. Ali imao sam sreće da mi predaje jedan dosta dobar profesor matematiku, tu nemam problema puno, ali mora da se radi. Tako isto i zaa programiranje, potrudi se sam koliko možeš, dođi do literature, vežbaj zadatke. Jeste da je dosta teže nego kada ti profesor pomaže, ali to ti je jedina mogućnost ako te programiranje interesuje. Ili uplati neki kurs ili privatne casove.

Ivance95, meni je ipak jednostavnije preko Binomne formule, sto ne znači da je teško pomoću Paskalovog trougla.

Aleksandre, ako mislis na ove identitete koje je saten napisala, to se radi u prvoj godini, kada se rade polinomi.